Konzultace 22. 10. 2020
Příklad 1: \( A = \{ 1;3;7;8 \}; B = \{ x \in Z - \{2;3;4\}; |x| < 5 \} \). Urči \( A \cup B \).
\( A = \{ 1;3;7;8 \} \)
\( \{ x \in Z; |x| < 5 \} = \{-4;-3;-2;-1;0;1;2;3;4 \} \)
\( B =\{ x \in Z - \{2;3;4\}; |x| < 5 \} = \{ -4;-3;-2;-1;0;1 \} \)
\( A \cup B = \{-4;-3;-2;-1;0;1;3;7;8\} \)
Příklad 2: \( A = \{ -2;-1;0;1;2;3;7;8 \}; B = \{ x \in Z - \{0;1\}; |x| < 5 \}; C = \{ x \in R; x>-1 \} \). Urči \( A \cap B \cap C \).
\( A = \{ -2;-1;0;1;2;3;7;8 \} \)
\( B = \{ -4; -3; -2; -1;2;3;4 \} \)
\( C = \{ -0.99;-0.98;0;1;... + \infty ... \} \)
\( A \cap B \cap C = \{ 2;3 \} \)
Příklad 3: \( A = \{x \in R; x>\frac{5}{4} \pi \} \cap \{ x \in Q; x< |- \frac{75}{9}| \} \). Urči, která čísla leží v množině \( A \).
\( \frac{5}{4} \pi \doteq 3.927 \)
\( \frac{75}{9} = 8.\overline{3} \)
Odpověď: Ve výsledné množině \( A \) leží všechna racionální (\(Q\)) mezi přibližně \(3.927\) a \( 8.\overline{3} \).
Příklad 4: Leží \( 2\pi \) v oboru racionálních čísel ( \( Q \) )?
\( 2\pi = 2 \times 3.1415998... = 6.283185307179586476925286766559... \). Toto číslo leží v oboru \( I \) a neleží v oboru \( Q \), protože nejsme schopní vysledovat periodu ani ukončit desetinný rozvoj.
Příklad 5: Leží \( 6.\overline{28} \) v oboru racionálních čísel ( \( Q \) )?
\( 6.\overline{28} = 6.2828282828... \). Toto číslo leží v oboru \( Q \), protože jsme schopní vysledovat periodu.
Příklad 6: \( \{ x \in N \} - \{ x \in N; x>5 \} \). Je tato množina konečná?
\( \{ x \in N \} = \{1;2;3;4;5;6;7;8;9;10;11;....\} \)
\( \{ x \in N; x>5 \} = \{6;7;8;9;10;11;....\} \)
Ano, tato množina je konečná. Má 5 prvků a vypadá takto \( \{1;2;3;4;5\} \).
Příklad 7: \( \{ x \in R \} - \{ x \in Q \} - \{ \pi \} - \{ \sqrt{2} \} \). Je tato množina konečná?
\( \{ x \in R \} = \{ x \in Q \} \cup \{ x \in I \} \)
\( \{ x \in Q \} = \{ x \in R \} - \{ x \in I \} \)
\( \{ x \in I \} = \{ x \in R \} - \{ x \in Q \} \)
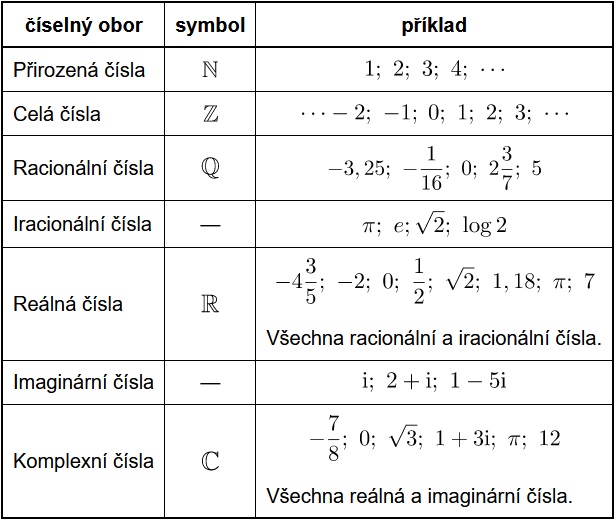
Jsem schopný najít nekonečnou množinu prvků, které patří do této množiny. Budou to všechny prvky množiny \( I - \{ \pi; \sqrt{2} \} \), tedy například řada prvků \( \{ \sqrt{3}; \sqrt{5}; \sqrt{6}; \sqrt{7}; \sqrt{8}; \sqrt{10}; \sqrt{11}; \sqrt{12}; ... \} \).
Ne, tato množina není konečná.
Příklad 8: Rozhodni, zda je prvek (\( \pi + 3.14 \)) součástí množiny \( \{ x \in R; x<2\pi \} \cap \{ x \in Q; x > \frac{68}{11} \} \).
Určení hraničních bodů:
\( 2 \pi = 2 \times 3.14159... = 6.28318... \)
\( \frac{68}{11} = 6.\overline{18} \)
Součástí této množiny jsou tedy všechny prvky oboru \( Q \) mezi \( 6.\overline{18} \) a \( 6.28318... \).
Tento prvek \( (\pi + 3.14) = (3.1415998... + 3.14) = 6.2815998... \) by teoreticky byl součástí výše zmíněné množiny, ale problém je takový, že tento prvek nemá ukončený desetinný rozvoj ani není možné vysledovat periodu, tudíž neleží v množině \( Q \), ale leží v množině \( I \). Průnik množin \( Q \) a \( R \) musí ležet v množině menší, což je množina \( Q \).
Prvek tedy není součástí množiny.
Příklad 9: \( \{x \in N\} \cap \{x \in Z\} = N \)
Příklad 10: \( \{x \in N\} \cup \{x \in Z\} = Z \)
Úvaha při řešení příkladů 9 a 10: viz Rozdíl oborů přirozených a celých čísel.